ちょっと脇道にそれてラグランジュ・ポイントの話をする。

前回の軌道シミュレーション・プログラムでは、100年後の小惑星の位置を計算させると、元々ラグランジュ・ポイント４と５に集まっていた小惑星が、ばらけてしまうと言うことを書いた。

ばらけてしまう理由は、本来、小惑星をラグランジュ・ポイントに集めている木星の引力を計算に入れていないからだ。

じゃあ、どうやれば計算に木星引力の影響を入れるかと言うのが、今回のプログラムasteroid2.rbだ。このプログラムも愛媛の実家で作った。前回のプログラムと同じようにダウンロードし、惑星や小惑星の軌道データの入っているフォルダ/ディレクトリで実行すると、木星と近い軌道半径を持った小惑星を50個だけロードし表示する。メニューの「編集」「日時の設定」を選び、目標の日時（未来に限る）を入力すると、アニメーションで動きだし、目標の日時まで計算したところで止まる。

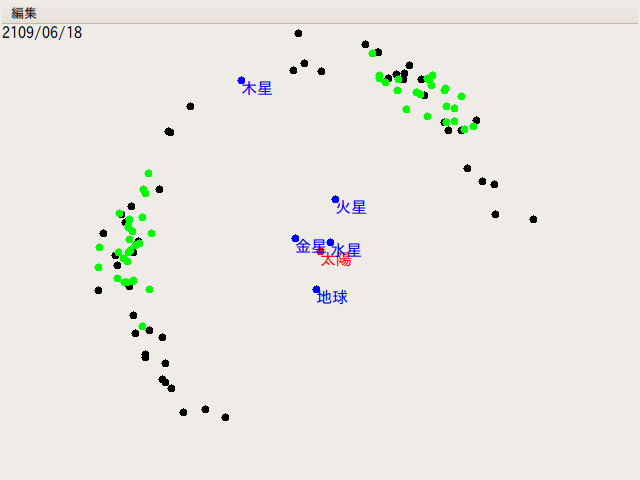
冒頭の画像は、そうやって、100年後の惑星・小惑星の位置を計算して表示したものだ。画像の中で黒い丸は、前回と全く同じ楕円近似で計算した小惑星の位置だ。これに対して、緑色の丸は、木星引力の影響を考慮した小惑星の位置である。見て判る通り、黒い丸はラグランジュ・ポイントから外れているが、緑の丸はラグランジュ・ポイントに集まったままである。

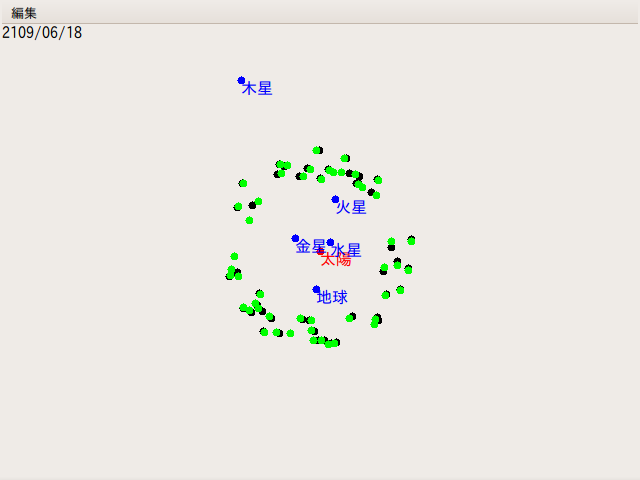
プログラム中の Radius の数値を 2.25 にすると、軌道長半径が 2.25AU 付近の小惑星を選ばれる。その100年後の位置が、2つ目の画像だ。多少ずれているところもあるが、黒い丸と緑色の丸の位置はほとんど変わっていない事が判る。これは、木星の引力の影響が積み重ならず、打ち消し合うためだ。ラグランジュ・ポイントの場合、軌道回転周期が木星と一致しているため、木星の引力の影響が積み重なるので、影響が大きいのである。

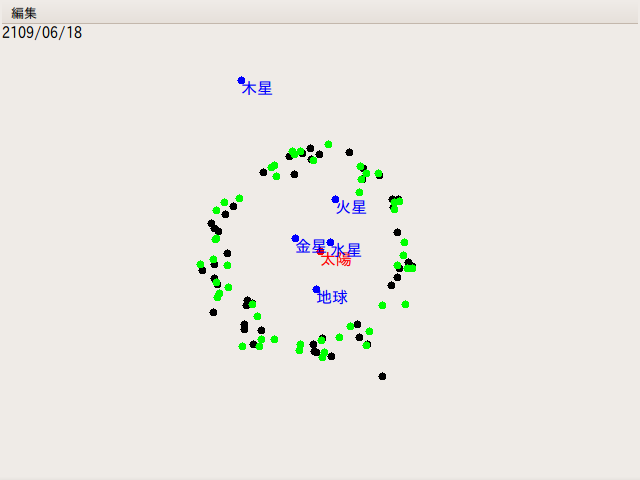
Radius の数値を 2.5 にして、100年後の位置を計算したのが、3つ目の画像だ。これも黒い丸と緑色の丸の位置が異なっている。実は、これらの小惑星の軌道周期は、木星の 3分の1 だ。ラグランジュ・ポイント４・５とは逆に木星の引力は積み重なりあって、小惑星を、この軌道からはじき出してしまう。

さて、今回のプログラムがどうやって計算しているかを説明しよう。今回のプログラムはルンゲ=クッタと言う方法で小惑星の位置・速度から引力の大きさを計算し、数値積分して位置を計算したものだ。

小惑星にかかる力は、太陽の引力と木星の引力を考慮している。それ以外の惑星の引力は計算していないが、他の惑星は木星に比べて小さいので余り影響が無いと考えた。もちろん、プログラムを改造して、他の惑星の引力の影響を計算することは可能だから、興味がある人は試すと良いだろう。

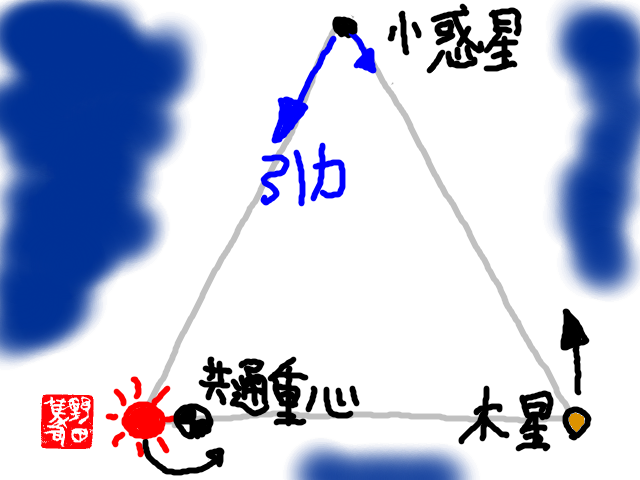
太陽と木星の引力を計算する時、太陽の場所は木星や小惑星の軌道の中心ではない。図に示したように、太陽と木星は、２つの共通重心を中心に互いを回っているようにした。図では大げさに描いたが、実際は、共通重心は太陽の中心から70万キロ強離れていて、太陽の表面から僅かに出ている場所だ。

70万キロと言うと大きな距離なようだが、太陽系スケールで言うとホンの僅かな距離で、木星軌道から見れば、0.1％程度だ。そのような僅かな太陽の位置のずれを考慮しないと、ラグランジュ・ポイントに小惑星は集まらない。太陽の位置のずれの計算は、プログラムの167〜169行にあるので、試しに、これらをゼロにすると、小惑星がラグランジュ・ポイントから離れて行くことが判る。

先ほどから、私は「木星の引力が影響して・・」と言ってきたが、本当は「木星の引力と 太陽の位置のずれが影響して・・」と言うのが正確だ。

プログラムでの計算ステップは、5日にしてある。つまり、小惑星にかかる引力を計算して、5日後の位置と速度を計算している。ただし、5日間同じ力がかかり続けるわけではなく、その間の変化を効率的に計算している。これが、ルンゲ=クッタと言うアルゴリズムだ。

10日後の小惑星の位置の計算なら5日ステップを2回繰り返し、100日後なら20回繰り返さす。いきなり100日後を計算するわけには行かない。

100年後なら7305回の繰り返しだし、小惑星50個なら、更に50倍の36万回以上だ。

わずか数年後の位置計算だとしても、とてもじゃないが、何十万個もある小惑星の計算などでやしない。とにかく、数値計算には時間がかかる。

私のプログラムに無駄があるが、それを治したとしても何倍か速くなるだけで、焼け石に水だろう。ruby のようなスクリプト言語ではなくて、コンパイラ言語にしても無駄だろう。抜本的には、グレープのような並列コンピュータを使わざるを得ないだろう。そこまで行かないでも、CUDAやOpenCLのようにGPUを使って並列計算するのも良いかもしれない。

でも、これ以上、数値積分プログラムを追求する気は無い。

数値積分をしなくても、楕円近似なら何年後でも、現実的な時間で小惑星の位置計算ができる。

要は、小惑星の軌道計算が十分な精度で行えれば良いだけである。

今回の積分計算プログラムで、ラグランジュ・ポイント４・５に小惑星を集めているのは、間違いなく木星の引力の影響である事が判り、楕円近似計算であろうが積分計算プログラムであろうが、少なくとも数十年程度であれば、大きな誤差が無い事が判った。だから、その範囲であれば、楕円近似計算で十分と判断できる。今回の積分計算プログラムは、それが判った時点でお役ご免。

じゃあ、なんで今回は、わざわざ今後使うつもりのない積分計算を細々と紹介したかと言うと、こういうのを限りなく改良してくと言うのが、コンピュータ・シミュレーションの入門者が陥りがちな事例だからだ。

コンピュータ・シミュレーションには、必ず誤差がある。どんなにプログラムを改良しても、誤差は残る。逆に言えば、限りなくシミュレーション・プログラムに改良する事ができて、それに応じてシミュレーションの精度は、どんどん良くなる。

頑張れば頑張るほど、精度は高くなるので、如何にも正しい事をしている気になってしまう。

だが、本来は、シミュレーションに必要な精度を見極め、それさえ達成すれば良いのである。

それを必要な精度も考えずに、闇雲に精度を限りなく高く・・・と陥ってしまうのだ。

まあ、何に使うかも判らずにシミュレーションにハマる人も多いけどね。

さて、愛媛の実家で作ったプログラムのストックも今回で終わり。

次回は、小惑星から小惑星に移る惑星間航行の軌道計算を紹介するつもりだが、これからプログラムを作らなければならない。次に暇ができてプログラムを作り込めるのが、いつになるか判らないから、次回が、いつになるかも判らない。

注意

ブログのコンテンツの内、「告知」など時期よって情報価値が無くなるのは除いてある。また、コンテンツに付いたコメントは書き込み者に著作権があるものと判断し、ここに持ってきていないので、コメントを見るときは、元々のブログコンテンツを参照してもらいたい。

その他、ブログ発表後、コメントなどの内容を反映するなど、内容を変更しているものもあるので、注意してほしい。