前回のコンテンツで、

「小惑星の数の平方根の逆数に比例している。計算時間は、小惑星の数の1.5乗と比例」と書いたが、何故、そのような関係になるかを考察した。

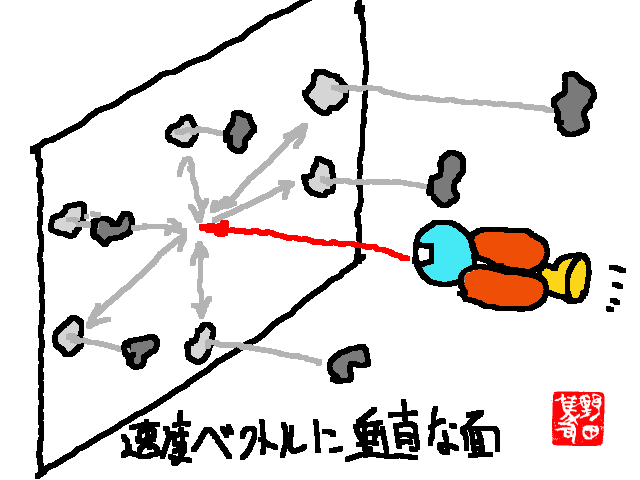
ある瞬間における宇宙船と小惑星との距離は、三次元的ものである。ところが、宇宙船が小惑星帯を通り抜けるような旅程全体での最短距離は、概念的には、イラストに示したように、速度ベクトルに垂直な平面への垂線との交点との距離になる。つまり、小惑星との距離は二次元的な直線距離になる。

小惑星の個数と各小惑星が平面で占有できる面積は反比例の関係になり、従って最短距離は小惑星の個数の平方根と比例することになのだ。

計算時間の話だが、私のアルゴリズムでは宇宙船の出発から到着まで一定時間間隔で計算しているのではない。最短にある小惑星までの近い時は細かい間隔で、遠い時は荒い間隔で計算している。具体的には、どんな事があっても最短距離の小惑星が宇宙船にぶつかって通り過ぎることの無いように、小惑星の速度の最大値（そこの太陽からの距離での第三宇宙速度）と宇宙船の速度との単純和速度で最短距離の小惑星までの距離を割った時間を計算時間の間隔としている。

つまり、計算回数は小惑星の平方根と比例するのだ。

また、一回の計算時間は単純に小惑星の数に比例する。

計算回数は小惑星の平方根と比例し、一回の計算時間は単純に小惑星の数に比例するわけだから、全体の計算時間は小惑星の数の1.5乗に比例することになる。

ここまでに、実は私が断りもなしに大胆な仮定をおいていることを、聡明な読者は気づいているかも知れない。その一つが「小惑星の動きに比較して宇宙船の相対的な速度が大きいこと」、もう一つが「宇宙船の速度ベクトルが直線的であること」である。

実は、これら二つの仮定は、少なくとも前回のコンテンツで示した地球〜木星のホーマン軌道においては、成立しているようである。と言うのも、前回のコンテンツの最後に示したグラフのように、小惑星の個数の平方根と最短距離は比例しているし、小惑星の個数の1.5乗と計算時間が比例しているからである。どうやら、宇宙船の速度ベクトルは、各時点時点でのベクトルを直線で近似しても良いようだ。

しかし、小惑星帯の中を、小惑星と同じ速度で周回している宇宙船だと、こうならないだろう。私の予想では、最短距離は小惑星の個数の立方根と比例し、計算時間は小惑星の数の1.33乗に比例すると思うのだが、まだ試していない。

注意

ブログのコンテンツの内、「告知」など時期よって情報価値が無くなるのは除いてある。また、コンテンツに付いたコメントは書き込み者に著作権があるものと判断し、ここに持ってきていないので、コメントを見るときは、元々のブログコンテンツを参照してもらいたい。

その他、ブログ発表後、コメントなどの内容を反映するなど、内容を変更しているものもあるので、注意してほしい。