ちょっと時間が開いてしまったが、小惑星シリーズの締めくくりとして、宇宙機に自由な軌道を設定して、小惑星との最接近距離を求める方法を説明しよう。

惑星間を航行する軌道は、ほとんどが無動力で慣性航行する楕円軌道か双曲線軌道が基本だ。「はやぶさ」のようにイオンエンジンを連続噴射する宇宙機は、むしろ例外的だし、はやぶさだって、旅程の大半は無動力の慣性飛行だ。ボイジャーが木星でスイングバイして軌道を加速した時も、木星近傍は木星を中心とした双曲線軌道で、地球と木星の間や木星と土星の間は太陽を中心とした楕円軌道か双曲線軌道で近似できる。

だから、好きな時点で地球などを出発し、好きな時に木星などの目的地に着く宇宙機の軌道を設計するには、出発時点での出発地点の座標と、到着時点での特着地の座標を調べ、その２点を結ぶ楕円なり双曲線を求めれば良い。

まず、出発地点と到着地点を求めるのだが、これは前回紹介した planet.rb を使えば良い。

ここでは、ボイジャー1号を例にしてみよう。

ボイジャー1号は1977年9月5日に打上げられた。この時の地球の座標：0.962257208885725 -0.300911514759908 -1.50980789430694e-05だ。

木星を通過したのは1979年3月5日だ。木星の座標：-3.21963186439629 4.19705755903192 0.0548123833933462だ。

さて、この２点を楕円で結べば良いのだが、はたと困ってしまう。一般的に言われているように惑星間飛行に「ホーマン軌道」を用いるのなら、出発地点と到着地点は、太陽を挟んで反対側つまり180度離れている必要がある。ところが、ボイジャー1号の場合、出発地点と到着地点は太陽を挟んで約145度離れている。つまりホーマン軌道として、ペリジ（近日点）とアポジ（遠日点）に出発地点と到着地点を配置するわけには行かない。

結局、出発地点と到着地点を通る楕円もしくは双曲線軌道の一部を通れば良いことになる。という訳で太陽を焦点の一つとする楕円もしくは双曲線軌道を描けば良いのだが、実は太陽を焦点の一つとする楕円もしくは双曲線軌道で出発地点と到着地点を通るものは無限にある。

しかし、無限にある楕円もしくは双曲線軌道の中で、1977年9月5日から1979年3月5日の日数である546日間で出発地点から到着地点に至る軌道は、たった一つしかない。この一つの軌道を見つけ出す方法は、18世紀の数学者・天文学者 Lambert （ランバートもしくはランベルトと発音）が彗星の軌道を決定するために発見し、その名前を取って Lambert 法と言われ、今でも使われている。

Lambert 法は発見から200年以上たっているので、色々な書籍で紹介されているが、

コロナ社 「イオンエンジンによる動力航行 (宇宙工学シリーズ)」

荒川義博監修 國中 均; 西山 和孝; 中山 宜典 (著)

で紹介されている計算式・アルゴリズムを参考に Ruby でプログラムした。

それが、lambert.rb で下記のようにコマンドすると、ケプラリアン軌道要素を返す。(コマンド部分は、一行で入力する)

$ ./lambert.rb 1977/9/5 0.962257208885725 -0.300911514759908 -1.50980789430694e-05 1979/3/5 -3.21963186439629 4.19705755903192 0.0548123833933462

546

a:763585605676.989 m = 5.10425453034184 AU

e:0.802476632588186

i：1.03009770256444 deg

Ω：-17.3174870361242 deg

ω：359.914809844918 deg

M:0.00244963340350288 deg

なお、残念ながら、「対象となる軌道は楕円軌道のみ」「1周回未満」「あまり長楕円になると収束しない」「精度はそんなに高くない」という欠点を持つが、概念的な検討には十分だろう。

上記のようなケプラリアン軌道要素を軌道生成にプログラミングしたのが、 asteroidInterval3V1.rb の 44行目から78行目の クラス SpaceCraft である。また、ケプラリアン軌道要素を軌道生成する変換式は、10年以上前から私のホームページ：基礎知識6　電卓で行う軌道解析・制御設計で公開しているので、これも参考にして欲しい。

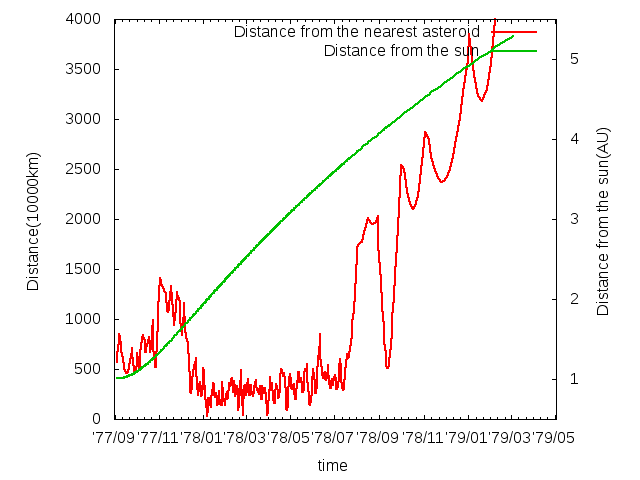
asteroidInterval3V1.rb を実行すると、53万個の既知の小惑星の内、最もボイジャー1号に近付くのは34万キロだと判る。グラフで表したのが、冒頭の図だ。

続けて、ボイジャー2号の地球から木星間の軌道を反映したのが、asteroidInterval3V2.rb だ。

さて、木星でスイングバイした後、土星に向かうボイジャーの軌道を求めようとしたのだが、残念がなら太陽系脱出速度を超え、双曲線軌道になるので、lambert.rb では軌道を求めることができない。

繰り返しになるが、惑星探査衛星や宇宙船の軌道を設計するときには、

1) 出発と到着の日時と、その時の出発と到着の座標を求める。

2) Lambert 法で、楕円もしくは双曲線軌道を求める。

その後、

3) ロケットで打上げ、地球近傍から双曲線軌道として地球引力圏から脱出、惑星間軌道に繋ぐ

4) 木星なりの目的地付近での双曲線軌道を通り、スイングバイとして通り抜けるか、減速制御で周回軌道に投入する軌道変換を計算する

5) 全体を数値積分にて、シミュレーションを行い、修正し最適化する。

6) 軌道投入や変更時の誤差を考慮し、軌道修正のシーケンスを整える。

と言う手順で、軌道設計を行う。

lambert.rb プログラムの双曲線対応やロケット打上げから地球引力圏脱出、目的地でのスイングバイや減速制御による周回軌道投入の説明は、いずれまた。

（暇ができたら書くけど、いつになるか判らないので・・・・）

注意

ブログのコンテンツの内、「告知」など時期よって情報価値が無くなるのは除いてある。また、コンテンツに付いたコメントは書き込み者に著作権があるものと判断し、ここに持ってきていないので、コメントを見るときは、元々のブログコンテンツを参照してもらいたい。

その他、ブログ発表後、コメントなどの内容を反映するなど、内容を変更しているものもあるので、注意してほしい。