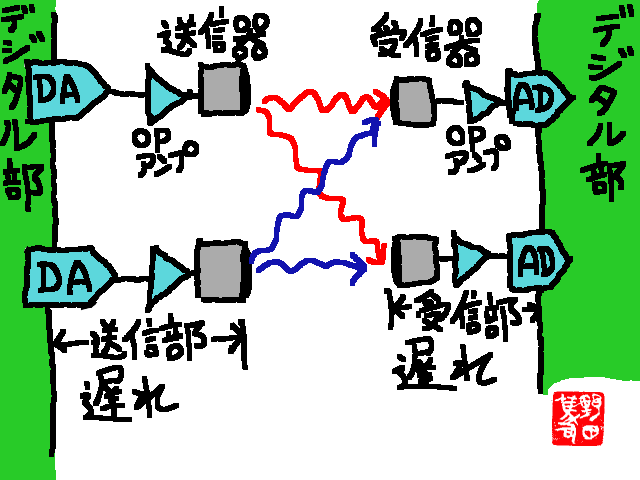
過去のブログで「水平方向の風向風速なら、送信部１つに受信部３つで良いが、垂直方向まで測定するときは、送信部３つに受信部３つとなる」と書いたが、これは安直だった。今一度、センサが何個必要か、考えなおしてみる。

超音波風向風速計は、送信器から出した超音波が受信器に届くまでの時間を計測して、それを元に風向風速を測る。無風なら、送信器と受信器の距離を音速で割った時間かかる。音速が340m/sとして、送信器と受信器の距離が34センチなら、その時間は、1msecだ。

送信器から受信器の方向に風が1m/sで吹いていると、超音波が341m/sで伝わるのと同じなので、2.9μsだけ早く到達する。逆方向に風が1m/sで吹いているなら、2.9μsだけ遅れる。

つまり、超音波風向風速計で風速を1m/sの精度で測りたければ、少なくとも2.9μsの精度で測定する必要があると言うことだ。実際には、2.9μsの10分の1の300ns程度の測定精度が要ることになる。

さて、測定精度を悪化させる誤差要因を冒頭のイラストを見ながら考えてみよう。まず、左右両端の『デジタル部』と書いた部分だが、ここの誤差は問題ない。デジタル部は50ns程度より大きい精度なら容易であり、今回要求される300nsの精度では全く問題ないと言える。

問題なのは、イラストの中で「送信部遅れ」と「受信部遅れ」と書いた部分と、イラストには無いが音速の変化である。これらは温度と気圧に依存するとされるので、通常なら温度と気圧を測るセンサを別に付けておいて補正するのが普通だ。

しかし、この方法だと、事前に温度特性を測っておかなければならないこと、温度と気圧センサが別個に必要になること、そのセンサにもそれなりの精度が要求される事が課題となる。

それなら、いっそ、温度や気圧で補正することなく、送信部から受信部に届く時間測定だけから、各誤差源の値も一緒に推定してしまえないか、それが今回のコンテツのテーマだ。

受信器数	送信器数
	1	2	3	4	5
1	1/6/6	2/6/7	3/6/8	4/6/9	5/6/10
2	2/6/7	4/6/8	6/6/9	8/6/10	10/6/11
3	3/6/8	6/6/9	9/6/10	12/6/11	15/6/12
4	4/6/9	8/6/10	12/6/11	16/6/12	20/6/13
5	5/6/10	10/6/11	15/6/12	20/6/13	25/6/14
6	6/6/11	12/6/12	18/6/13	24/6/14	30/6/15

表を見てもらいたい。縦の列は送信器の数が1〜5個の場合、横の行は受信器の数が1〜6個の場合の表になっている。

表の中のスラッシュ”/”で区切った数字の一番左は、測定できるパラメータの数。つまり、送信器から出した超音波が受信器に届くまでの時間の数で、当たり前だが、送信器数と受信器数の積になっている。

真ん中の数字は、直接できない未知のパラメータの数。全て「６」になっているのは、内訳が以下の通り

・音速

・風向風速（３次元的なベクトル要素なので、パラメータは３つ）

・送信部の遅延時間（全ての送信部の遅延は同一と仮定）

・受信部の遅延時間（全ての受信部の遅延は同一と仮定）

右側の数字は、同じく直接できない未知のパラメータの数なのだが、この場合は、送信部、受信部ともに全て遅延が異なると言う仮定を置いている。

送信部と受信部の遅延時間は、温度に依存すると思うから、同一回路で同一部品なら同じ遅延時間になりそうな気もする。一方、部品一個一個特性が違う可能性もあり、どちらが支配的かは実測してみないと判らない。

とりあえず、測定できるパラメータの数だけ連立方程式が立てられる。未知のパラメータの数が連立方程式の数より多ければ、解は得られない。これを赤字で書いている。ところどころにある黒字は、連立方程式の数が一つ足りないが、風向風速を水平面だけのパラメータとすると成立するもの。

青字で書いたところが、連立方程式の数が未知のパラメータの数より多いので、解が得られる可能性がある。「可能性がある」と、やや曖昧な書き方をしたのは、連立方程式によっては、数が多くても解が得られない場合があるから。これは、送信器と受信器の配置によって、連立方程式が解きやすいものと解きにくいものが出てきてしまう。言い方を変えると、「表中、赤字の部分は幾ら考えても無駄。青字の部分は連立方程式の解きやすい配置を考える余地がある。」と言うこと。

今のところ、送信器２個と受信器３個の組合せが最有力と考えている。これは、送信部同士、受信部同士が同じ遅延特性だと言う仮定なら解が得られるのと、STM32F4はDACを２つ、ADCを３つ内蔵しているので回路が簡単に済むからだ。

送信部と受信部の遅延特性が個々に異なるなら送信器４個と受信器３個が有力かな？この場合、DACとは別に送信器をON/OFFする信号を与えて、４つを切り替えて使うもの。切り替え時間が短ければ、遅延特性とかが変化することは無いだろうと考えてだ。

と、ここまで読んでいて、「スラッシュ”/”で区切った数字の真ん中と右の数字の色は判ったけど、左端の数字の色は何だ？」と思った人は注意深い！！

左端の数字は４以上だと青字になっているけど、何の意味があると思う？

実は、今までの話はあくまでも、瞬間的に取ったデータだけで連立方程式を解いた場合の話。しかし、実際は、時々刻々とデータを取っていけば、連立方程式の数が増える。もちろん、風が全く吹いていなかったり、同じ風向風速の風が吹き続いていても、実質的には連立方程式の数が増えないので解は得られない。

しかし、風の強さや向きは変わる方が普通だ。その変化は、温度や気圧の変化より早い。

つまり、同じ温度と気圧で、送信部や受信部の遅延時間が変わらず、音速も変わらない状況下で、風の強さや方向が変わる度に連立方程式が増えていく。もちろん、風向風速が変わると未知のパラメータも３つ増えるけど、測定できるパラメータが４つより多ければ、いずれは連立方程式の数が未知のパラメータより多くなると言うわけ。左端の数字は４以上の場合に青字で書いてあるのは、これ。ある程度の量が得られたら、解が得られて、風向風速も遅延時間も音速も判る。

これは、最小二乗法って言う方法なんだけど、これなら送信器２個、受信器２個ですむ。STM32F4の性能なら、オンボードで最小二乗法を行うことも可能だろう。

どの方法で、どの組合せがベストかは、今後の課題だ。

注意

ブログのコンテンツの内、「告知」など時期よって情報価値が無くなるのは除いてある。また、コンテンツに付いたコメントは書き込み者に著作権があるものと判断し、ここに持ってきていないので、コメントを見るときは、元々のブログコンテンツを参照してもらいたい。

その他、ブログ発表後、コメントなどの内容を反映するなど、内容を変更しているものもあるので、注意してほしい。