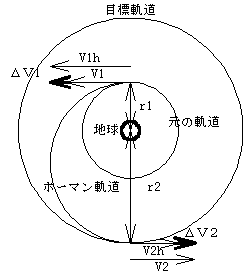
すなわち、軌道制御を遠地点(アポジ)と近地点(ペリジ)に限定し、制御時間をゼロに近似
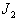 項まで(長周期摂動のみ)
項まで(長周期摂動のみ)
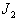 項まで(長周期摂動のみ)
項まで(長周期摂動のみ)
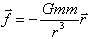
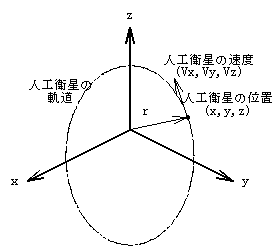
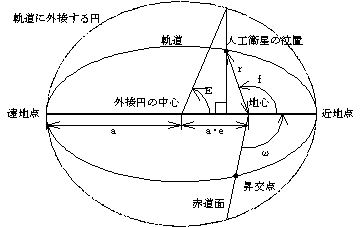
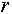 は地心からの距離、
は地心からの距離、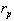 は最も近いときの距離)
は最も近いときの距離)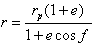 ・・・(1)
・・・(1)
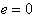 で円軌道
で円軌道
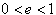 で楕円軌道
で楕円軌道
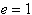 で放物線軌道
で放物線軌道
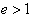 で双曲線軌道 (以降の説明では、
で双曲線軌道 (以降の説明では、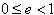 のみを対象とする。)
のみを対象とする。)
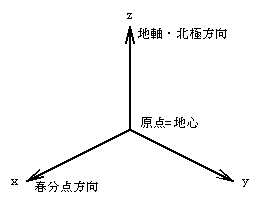
 ・・・(2)
・・・(2)
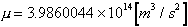
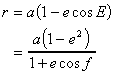 ・・・(3)
・・・(3)
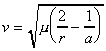 ・・・(4)
・・・(4)
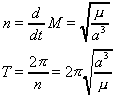 ・・・(5)
・・・(5)
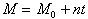 (
(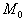 はEPOCHでの平均近点離角)
はEPOCHでの平均近点離角)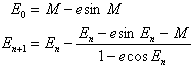 ・・・(6)
・・・(6)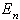 をイタレーションの結果から求める。上式を、3~6回も繰り返せば、実用上問題ない程度には収束するはずである。
をイタレーションの結果から求める。上式を、3~6回も繰り返せば、実用上問題ない程度には収束するはずである。
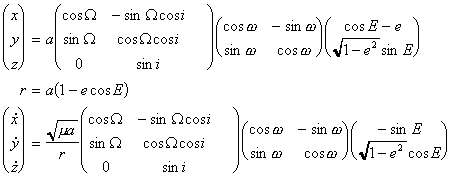 ・・・(7)
・・・(7)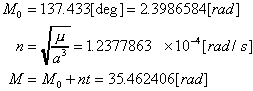

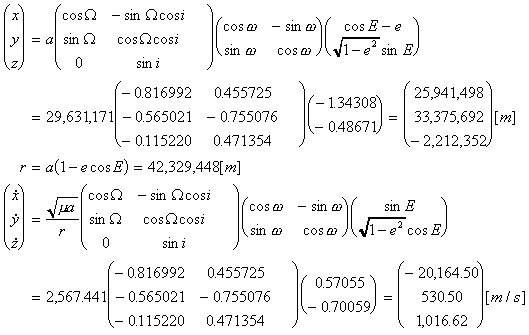
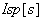
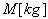
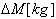
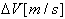
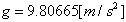
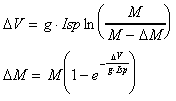 ・・・(8)
・・・(8) は次の様になる。
は次の様になる。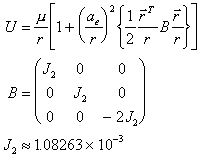 ・・・(9)
・・・(9)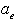 は地球の赤道半径であり、次のような値となる。
は地球の赤道半径であり、次のような値となる。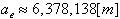
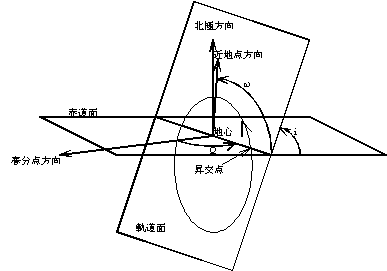
衛星の軌道面及び近地点は、次のようなレートで回転する。
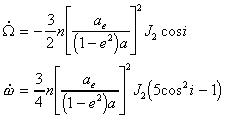
また、変化のイメージを図5に示す。

 ・・・(11)
・・・(11)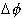 とする。
とする。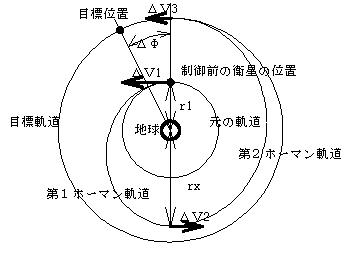
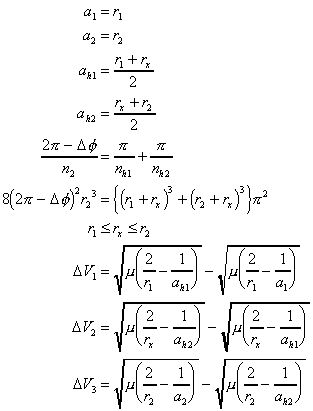 ・・・(12)
・・・(12) ・・・(13)
・・・(13)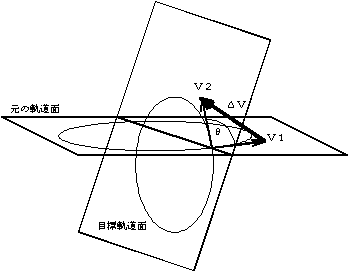
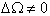 の場合、まず、「J2項による長周期摂動」で示したようなΩの変化を利用し、Ωを合わせる。次に、
の場合、まず、「J2項による長周期摂動」で示したようなΩの変化を利用し、Ωを合わせる。次に、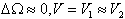 として、式(14)で示される増速を、赤道面上(昇交点or降交点)で行うことが多い。
として、式(14)で示される増速を、赤道面上(昇交点or降交点)で行うことが多い。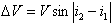 ・・・(14)
・・・(14)
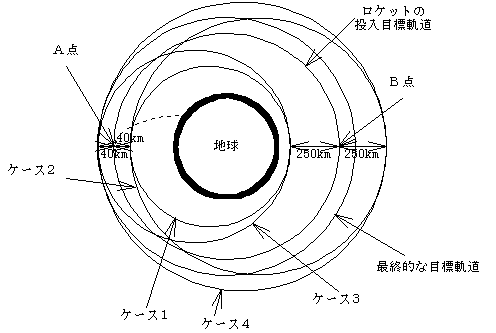
| ±40km(投入点) ・・A点 ±250km(投入点から半周)・B点 |
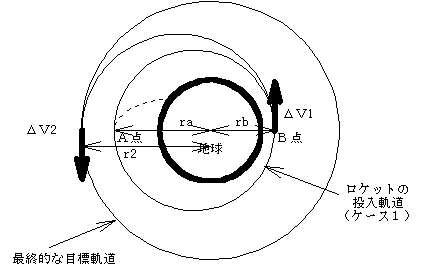
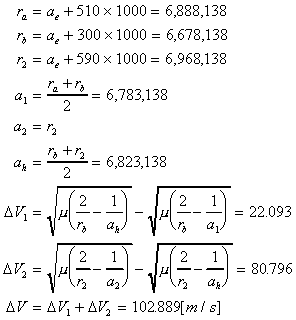

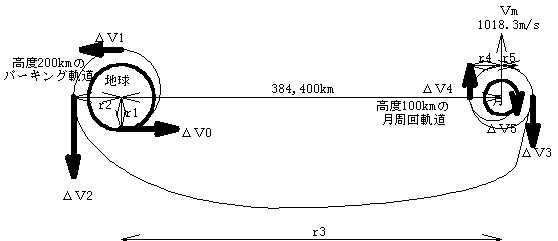
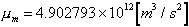 、月の軌道半径1,738.4kmである。
、月の軌道半径1,738.4kmである。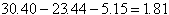 度の最小の組み合わせを考慮する。
度の最小の組み合わせを考慮する。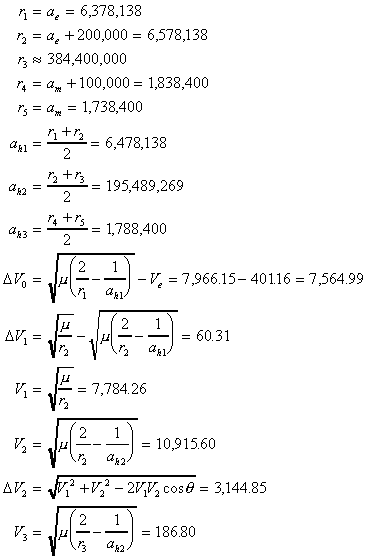
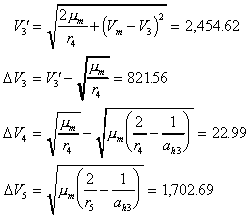
| 7,564.99 60.31 | |||||
| 3,144.85 | |||||
| 821.56 | 315.3 | 2600.00 | 606.66 | ||
| 22.99 | 315.3 | 1993.34 | 14.77 | ||
| 1702.69 | 315.3 | 1978.57 | 837.80 | ||
| 1140.77 | 1459.23 |