概要
基礎研究や斬新な技術開発が生み出す価値の確率分布は、ガウス分布ではなく、べき乗分布だと推測した
しかし、もし、本当に「べき乗分布」なら、なぜ今まで判らなかったのか?
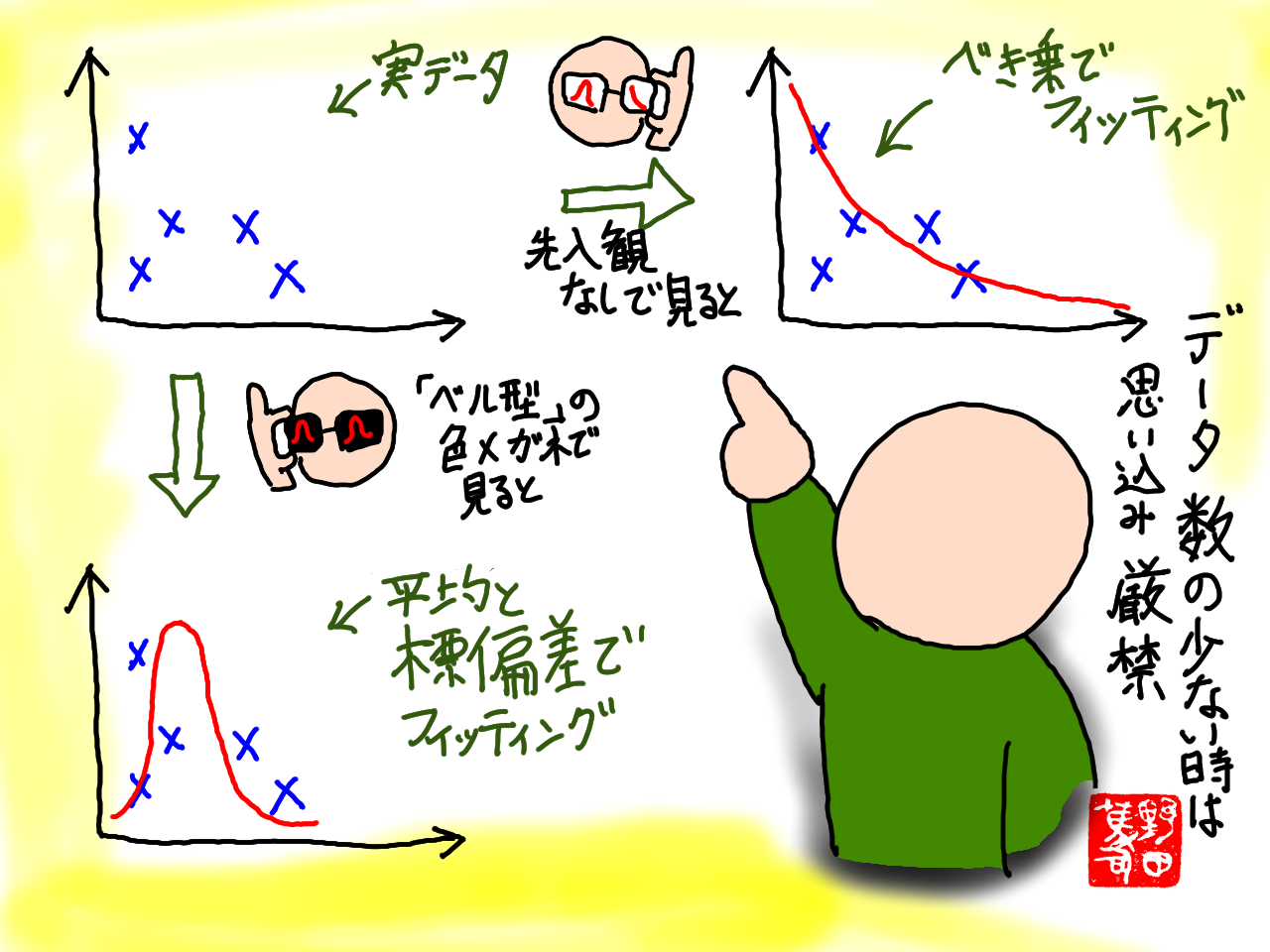
このページでは、「ガウス分布(ベル型)を信じ切っている人」には、「べき乗分布」も「ベル型」に見えると言うことを示す。
なぜ、べき乗分布してるなら、なぜ誰も気付かなかったのか?
前の頁に、「選択と集中」が間違ったのは、ガウス分布(ベル型)してなかったからを示したが、もし、本当にべき乗分布しているなら、何故、誰もそれに気づかなかったんだろうか?
そこで、基礎研究や斬新な技術開発が生み出す価値のが、べき乗分布するシミュレーションを行い、それをベル型を信じている人が、どう受け止めるかを考えてみよう。
シミュレーションに使うパラメータ
べき乗分布の場合 その3の所謂「2 8 の法則」に当てはめてモンテカルロシミュレーションを行う
すなわち、L = 、M = 、N = 、
、
、
を使ってみる。
モンテカルロシミュレーション
ベル型を信じている人は「選択と集中」戦略を取るだろうと言うことで、多くの候補の中から選抜された 人ずつに分配を回試す。
なお、ここでは、研究や技術開発の期間が1年間として、その価値も1年で出てくると仮定している。
これは、試行の全てを平均化すると、人に分配するので、儲けがプラスになる
ここでは、試行の1回毎に、平均と偏差を計算する。
これをどう見るであろうか? むしろ、4回目と8回目の標準偏差が大きすぎて、ここでは『まぐれ』が起きていると判断するのが、普通かもしれない
判り易い数字に
先の例では余りに小数点が多いので、具体的な数字を入れてみよう(モンテカルロシミュレーションの『乱数』は全く同値である)
例えば、予算円を人に円ずつ分配する。 一定期間後(ここでは、1年後と仮定)に得た価値(利益ではないよ)をモンテカルロシミュレーションで
回試す
1年目は赤字
1回目の試行では、最も価値を生み出した人でも円である。元々円配分されているので、円の赤字と言っても良い。
最も悪い成績の人に至っては、円、円の赤字である。
1回目の試行の価値の合計は、円、円の赤字である
ベル型信仰の人なら、平均と標準偏差を求めるだろう。平均は、円、標準編は円である。 おそらく、この平均と標準偏差の導出方法には疑問すら抱かないだろう、
ベル型信仰の人は。
人 試行1年目の終わり、経営者・管理職が評価をしたら、この試みは完全に失敗と思うだろう
人全員が、分配された円を下回る価値しか得られず、全員の得た価値の合計は、最初の予算の 1/3 にも満たないのだから。 ほとんどの場合、この試行は失敗と判断され、2年目以降は中止されるだろう。
もしくは大きくルールを変更する
ルールを変更する時、おそらく『選択と集中』の方向に舵をきるだろうが、べき乗分布の場合、事態を悪化させるだけである
と思われる
2年目も 3年目もは赤字
経営者・管理職がとても忍耐強く、寛容で、2年目も同じ試行が行われたとする。 2年目は、最も価値を生み出した人は、
円にもなり、分配された金額の2.5倍にもなる。 しかし、それ以外の人は、分配された金額よりも少ない価値しか生み出せず、合計は
円と予算の半分しか回収できない。
4年目は黒字、しかし、それまでの4年間の総計では赤字
経営者・管理職が、信じられないほど忍耐強く、寛容で、3年目以降も試行を続けられたとしよう。 3年目も同じく赤字が続くが、4年目に異変が起こる。 上位2人が、分配された金額より多く価値を生み、その結果、合計で
円と、初めて黒字になる。
4年目に黒字を出したからと言っても、ほんの僅かなものである。 それまでの 4年間に生み出した価値の合計で円であり、4年間に使った予算の合計円と比べると、依然として、赤字である。
4年目に黒字を出したことだし、この辺でやめよう・・と言う話になりそうな気もするが、経営者・管理職が、またまた忍耐強く、寛容で、5年目以降も試行が続けられたとしよう。 5年目、6年目、7年目とも相変わらず、赤字が続く。
8年目は奇跡の年に奇蹟
しかし、8年目に奇蹟が起きる。 なんと、5人が分配された以上の価値を生み、特に上位の2人は、極端に高い価値を生み出す。 最も価値を生み出した人は 円、2人目でも 円であり、この年の合計は、円と大きく黒字になる
10年間の総計では黒字、しかし・・・
この後、9年目、10年目も赤字が続く とりあえず、10年間続けた結果、10年間の合計は 円であり、この間にかけた予算の合計 円より大きく、総計では黒字になる。 この10年間の各個人の生み出した価値の平均は、
円で、標準偏差は円だ。
えっ? 平均より標準偏差が何倍も大きい! これは何か異常なんじゃないか!?
10年間の総評価、しかも間違っている
10年間の業績を分析
この『分析』とは、『正しいデータ』を『ベル型と言う間違ったテンプレート』に当てはめる行為だ
してみると、8年目の上位2人が生み出した価値の合計が、円であり、この2人の業績を除くと、価値の合計は円と赤字に転落する。
この2人が異常であり、取り除いた方が統計的に正しいんじゃないか? トップ2人の業績を除く、各個人の生み出した価値の平均は、
円で、標準偏差は円だ。 これでも、平均より標準偏差の方が大きいが、最初の値よりはマシだ。 トップ2人の業績を除いた平均と標準偏差で計算すると、トップ1人目は、
σ、2人目はσになる。 (ちなみに、トップ2人を含めた平均と標準偏差で計算しても、トップ1人目は、
σ、2人目はσだ。)
これらのσ値は、確率的にあり得ない数字
正規分布(ガウス分布)の累積分布 数値計算でも示したが、ベル型(ガウス分布)の累積分布関数の一般解は存在しないため、極端に大きなσ値の存在確率を求めることは難しいが、少なくとも 8σ以上の存在確率は『在り得ない』と言えるほど小さい。
である。従って、トップ2人を異常データとして、統計から削除するのは、適当と思われる。この2人のような異常な状態でかろうじて黒字になっている試行など危うくて続けるべきではないというのだ
もう一つの解釈
もちろん、間違った解釈だ
がありえる。
「8年目に、2人も異常に高い価値を生んでいるのは偶然ではないはず
Javascriptでプログラムを作っているので、ソースコードを見てもらえば判るが、私は、XorShift と言う一般的な乱数で、シード(乱数の種)も1と言う余りにも一般的な乱数を使ってモンテカルロシミュレーションを行っているだけだ。「偶然」と言うより「べき数分布」はこうなると思った方が良い。ましてや「他の要因」がある筈もない
だ。何か他の要因(管理の仕方とか、指導者が良かったとか)がある筈だ。それを調べて再現してみよう」と言う事になる。
100年間の続けるのが正解
どんなに辛抱強い経営者でも、10年間でやめてしまうだろう。もしくは、継続するとしても、ルールを大きく変えるであろう。
しかし、これを100年間続ける方が正しい。 100年間に生み出した価値の合計は
円となり、投入された予算の合計円を大きく上回る
個人で、100年間に最も高い価値を生み出した人は、円にもなる。 最初の10年間のトップの5倍以上だ。