概要
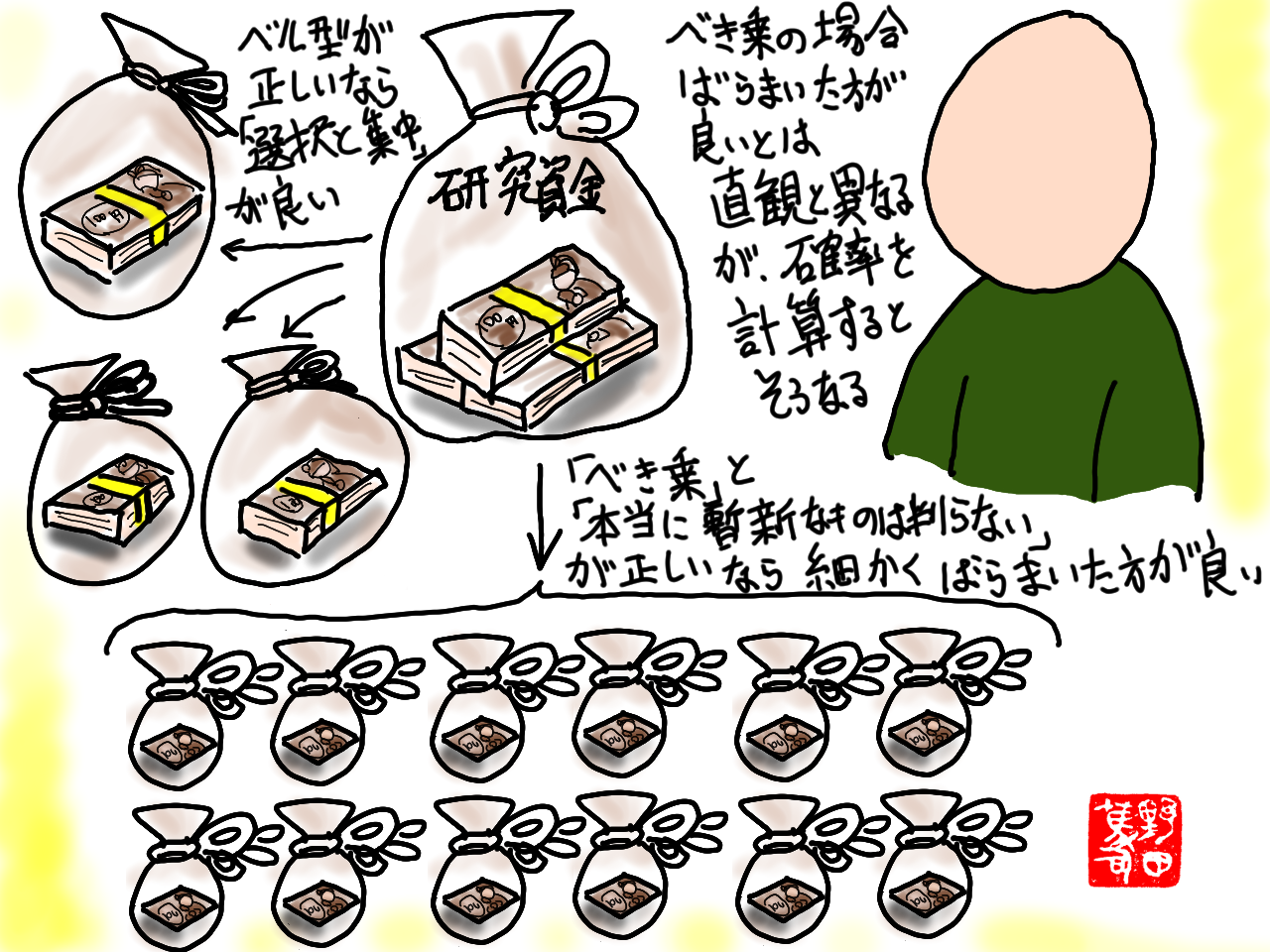
基礎研究や斬新な技術開発が生み出す価値の確率分布は、べき乗分布だと推測した
もし、そうなら、細かく分配した方が良いことになる。
その傾向をモンテカルロシミュレーションを使って示す。
シミュレーションに使うパラメータ
前回と全く同じ条件、つまり べき乗分布の場合 その3の所謂「2 8 の法則」に当てはめてモンテカルロシミュレーションを行う
すなわち、L = 、M = 、N = 、
、
、
を使ってみる。
この条件で、正しい分配法
(数学的に証明された)真の意味での「最善の方法」ではないかもしれないが、少なくとも「ベル型信仰の人が行う」よりも正しい分配方法と思ってほしい
でのシミュレーションを行う。
モンテカルロシミュレーション
「正しい分配方法」と言っても、考え方単純である。 より、多くの人に分配すれば良いのだ。 もちろん、一人当たりの配分は減るが。
前回と同じ、予算円を、今度は『多くの提案者から選抜しない』で、提案者全員の人に円ずつ分配する。 1年毎に得た価値(利益ではないよ)をモンテカルロシミュレーションで
年間回試す。
今回は、配分する人数が多いので、全員の分ではなく、各年度のトップ3位までと全体合計のみを表に示す。
全体として
上の表に示したように、5年目と6年目は単年度では赤字だが、累積では常に黒字であり、10年後には、予算総計の1.7倍の価値を生み出している。
10年間、都合人のトップの生み出した価値は円でり、分配された円に対して、倍もの価値を生み出している。
トップ3人の合計は、円であり、% の人が、全体の% の価値を生んでいる。 イノベーションは、「千に三つ」との言葉通りである。
トップ20人の合計は、円であり、% の人が、全体の% の価値を生んでいる。
トップ200人までが配分された以上の価値を生んでおり、その合計は、円であり、% の人が、全体の% の価値を生んでいる。 これは、2 8の法則、つまり「2割の人が、8割の利益を生む」だ
トップの11人を除いた利益(生んだ価値-予算)が円と黒字だが、トップの12人を除いた利益が円と赤字になる。 つまり、全体の
% が居ても、赤字になってしまう。
このように多くの人が価値を生まないと言う問題があるものの全体としては、上手く行くことが判る。
直感と合わない?
上のグラフを見て、1番に感じることは、「直感と合わない」ことだろう。
- なぜ、「選抜された人に高額の研究資金」を与えたより「選抜しない人に少額の研究資金」の方が、高い成果を出すのか?
- なぜ、投入された研究資金よりも、ずっと多くの成果の価値が生まれるのか?
- 本当に「べき乗分布」するのか?
- そもそも、このシミュレーションがインチキなのでは?
最初に断っておくが、シミュレーションにおいて、なんのインチキもしていない。
実は、このページに限らず、ほとんどのページのプログラムは、JavaScriptでクライアントサイドでリアルタイムで動いている。
正規分布(ガウス分布)の累積分布 数値計算だけは、予めRubyプログラムで計算させた結果を表示している。もし、クライアントサイドで行ったら、何時間もWebブラウザがハング状態になるだろう
だから、ページのソースを見れば、プログラムの中身も判る。
これは、プログラムに何の恣意的なものが含まれないことを示すためでもある。
また、乱数は、「XorShift」と言う一般的な手法を用い、シード(乱数の種)も「1」を使っている。
パラメータなど、いろいろ試してみたい人は、このページのソースをダウンロードして改変して良いが、『付録:シミュレーション』を用意しているので、そこで試すと良い。
『なぜ、「選抜しない人に少額の研究資金」の方が、高い成果を出すのか』に関しては、『べき乗分布とはそういうもの』としか言いようがないし、『なぜ、研究資金よりも、ずっと多くの成果の価値が生まれるのか』については、『科学技術の進歩と言うのは、「0から1の価値を生む」』と言う本質を理解していないと言うことだ。
これら2点については、「従来の常識に囚われすぎ」で、根本は教育問題と思われるが、問題の根が深すぎるので、ここではこれ以上扱わない。いずれ何処かで纏めて説明したい。
(まあ、私も「研究や技術開発の成果」が僅か1年で価値が出るという仮定は短すぎるような気もしているが)
べき乗分布の場合のパラメータ推定
べき乗分布における分配の最大の問題は、「本当に べき乗分布しているか? べき乗分布しているなら、その分布パラメータをどう推定すれば良いか?」であることは疑いの余地はない。
詳細は、べき乗分布の場合のパラメータ推定に示すが、下のグラフにシミューレション結果を示すように、実際にデータを取得し、概ねサンプル数が1000を超えれば、パラメータが推定できることが判る。
すなわち、「研究や技術開発の成果が、研究資金の何倍になるか」のデータを1000以上のサンプル数取れば、証拠になることが判る。